
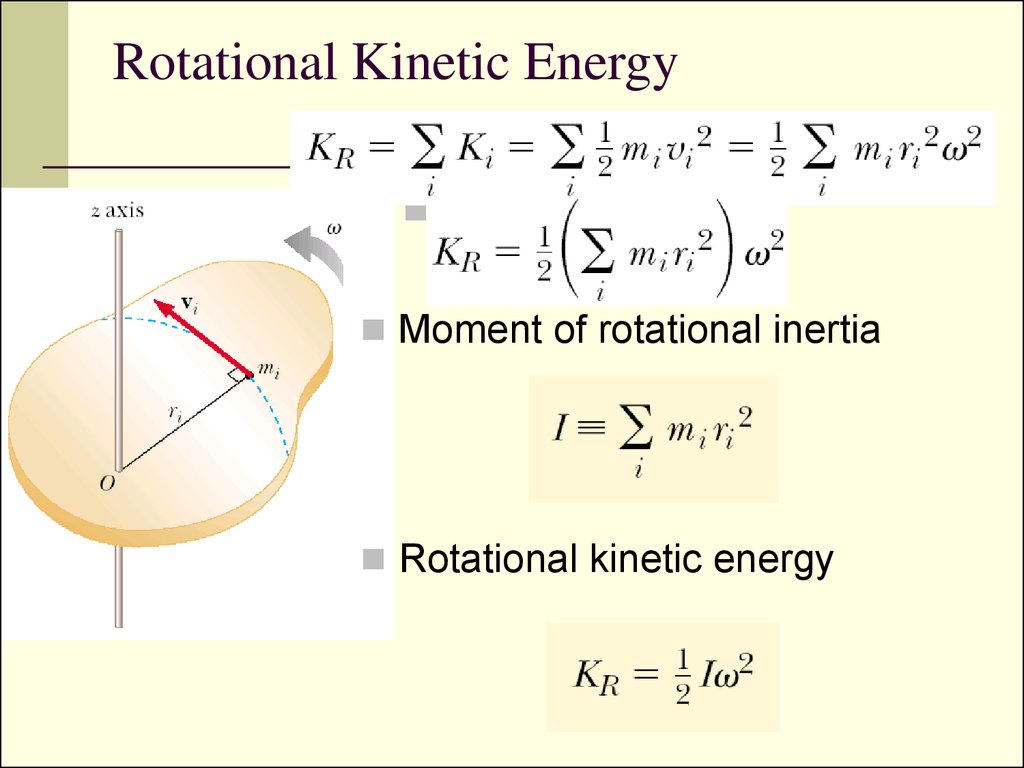
The moment of inertia of any object about an axis through its CG can be expressed by the formula: I = Mk 2 where I = moment of inertia R= distance from the point mass to the reference axis Determining the Radius of Gyration
M = mass of element (Slugs or other mass unit) Where I = MOI (slug-ft 2 or other mass-length 2 units) MOI, sometimes called the second moment, for a point mass around any axis is: I = Mr 2 Value of g : 32.17405 ft/sec 2 or 386.088 in/sec 2ĭo not use local value of g to convert to mass! What is the Moment of Inertia Formula? If moment of inertia or product of inertia are expressed in the following units, then their values must be divided by the appropriate value of “g” to make them dimensionally correct. Slug-ft 2, lb-in-sec 2, kg-m 2, lb-ft-sec 2, oz-in-sec 2 If moment of inertia or product of inertia are expressed in the following units, then their values can be used in engineering calculations as they are: are lb-in 2 , even though this is dimensionally incorrect. Slug-ft 2 slug = mass dimensionally correct Lb-in-sec 2 lb-in-sec 2 = distance 2 x weight/g weight/g = mass dimensionally correct Lb-in 2 lb = weight must be divided by g = 386.088 in/sec 2 The following table shows some of the units in use today for moment of inertia and product of inertia: Again, dimensional analysis will confirm if correct units are being used. When lb-in 2 or lb-ft 2 are used to define MOI or POI, the quantity MUST be divided by the appropriate value of “g” to be dimensionally correct in engineering calculations. Correct units of moment of inertia (as well as product of inertia) are: MASS x DISTANCE 2. This leads to units of moment of inertia such as lb-in 2, where the “lb” refers to the weight of the object rather than its mass. However, for reasons which have been lost in antiquity, in the USA an object weighing 1 pound is often referred to as having a mass of 1 pound. If the unit of weight is the pound, then the unit of mass cannot also be a pound, since this would violate Newton’s second law. In the United States, the word “pound” is often misused to describe both mass and weight. Values for moment of inertia can only be positive, just as mass can only be positive.īrowse MOI Instruments Units of Moment of Inertia Values for center of gravity can be either positive or negative, and in fact their polarity depends on the choice of reference axis location. This axis can then be translated to another axis if desired, using the rules outlined in the section entitled “Parallel Axis Theorem”. If the reference axis will be used to calculate moment of inertia of a complex shape, choose an axis of symmetry to simplify the calculation. If the object flies in space, then this axis is a “principal axis” (axis passing through the center of gravity and oriented such that the product of inertia about this axis is zero (see discussion of product of inertia). If the object is mounted on bearings, then this axis is defined by the centerline of the bearings. Although any axis can be chosen as a reference, it is generally desirable to choose the axis of rotation of the object. Three reference axes are necessary for calculating center of gravity, but only one axis is necessary to define moment of inertia. T = IA (T = torque I = moment of inertia A = rotational acceleration) Choosing the Reference Axis Location even on a Complex Shape The greater the distance the mass is from the center of rotation, the greater the moment of inertia.Ī formula analogous to Newton’s second law of motion can be written for rotation:į = Ma (F = force M = mass a = linear acceleration) Unlike inertia, MOI also depends on the distribution of mass in an object. Moment of inertia is, therefore, rotational mass. Inertia can be thought of as another word for mass. Inertia is the tendency of an object to remain at rest or to continue moving in a straight line at the same velocity. Moment of inertia is similar to inertia, except it applies to rotation rather than linear motion. However, in real life, unless the axes are well defined and can be accurately referenced, the moment of inertia calculations are meaningless. Theoretically, these axes can be at any location relative to the object being considered, provided the axes are mutually perpendicular. The accuracy of the calculations (and of the measurements to verify the calculations) will greatly depend on how well the axes are defined. The first step to calculate moment of inertia for a mass is to establish the location of the X, Y, and Z axes.
#Rotational dynamics calculator how to#
How to Calculate Moment of Inertia (MOI) in the Real World


 0 kommentar(er)
0 kommentar(er)
